패리티 비트
패리티 비트 방식은 추가되는 비트가 적으면서 오류가 발생한지 검사할 수 있는 효과적인 방식임
대표적 방법은 오류 검출을 위하여 아스키 코드 7비트에 패리티 비트를 추가하여 8비트로 구성하는 방식임
패리티 비트를 추가하는 방법은 짝수 패리티, 홀수 패리티 2개가 존재함
이때 짝수와 홀수를 구분하는 것은 비트들의 1의 갯수를 말함
즉, 1을 3개로 맞춤 = 홀수 패리티, 반대는 짝수 패리티임
EX---
아스키 G = 1000111
짝수 패리티 = 0
홀수 패리티 = 1
해밍 코드
패리티 비트를 이용하는 경우에 수신한 데이터가 오류가 있다는 것은 0, 1로 이루어진 data중 어느 부분이 오류가 나서 반전되었다는 것이다.
이때 이 위치를 확인해서 반전시키면 다시 원복이 가능함
이를 찾기 위한 코드를 오류-정정 코드라고 부르며, 가장 많이 사용하는 것이 해밍 코드임
해밍코드란,
데이터 비트의 수에 따라 다수의 패리티 비트를 추가하여 오류가 방생한 비트의 위치를 찾는 방식임
이때 필요한 패리티 비트의 수를 k, 데이터 비트의 수를 d라고 했을 시, k는
2^k -1 >= d + k
의 식을 따름
예시로 데이터가 4개라면
2^k - 1 >= 4 + k가 되는데, k가 3이라면 7 >= 7이 되어 필요한 페러티 비트는 3개인것을 확인할 수 있다
결과적으로 4비트의 데이터를 해밍 코드로 변환하면 4개의 데이터 비트, 3개의 패러티 비트가 사용되어 총 7비트의 코드가 되는것이다.
이때 4개의 데이터 비트를 D1~4로 부르게 되며, 페러티 비트는 p1, 2, 4가 되게 된다
이들은 이하의 표와 같이 배치된다
| 비트 번호 | 7 111 |
6 110 |
5 101 |
4 100 |
3 011 |
2 010 |
1 001 |
| 해밍 코드 | D4 | D3 | D2 | p4 | D1 | p2 | p1 |
이때 p에 해당하는 부분을 보면 모두 1이 1개인것을 확인할 수 있다
각 패리티 비트의 값은 그 비트와 같은 위치에 1이 존재하는 비트 번호를 가진 데이터 비트들에 대한 짝수 패리티 값으로 세팅된다.
p1 = 첫 자리가 1인 비트들 = 3, 5, 7
p2 = 두번째 자리가 1인 비트들 = 3, 6, 7
p4 = 세번째 자리가 1인 비트들 = 5, 6, 7
이때 기본값으로 짝수 패리티를 사용한다
EX---
보내진 데이터가 1100일시
| 비트 번호 | 7 111 |
6 110 |
5 101 |
4 100 |
3 011 |
2 010 |
1 001 |
| 해밍 코드 | 1 | 1 | 0 | p4 | 0 | p2 | p1 |
p1 = 3, 5, 7 = 0 0 1 => 짝수 패리티 = 1
p2 = 3, 6, 7 = 0 1 1 => 0
p4 = 5, 6, 7 = 0 1 1 => 0
그리고 해당하는 위치에 값을 넣어준다
| 비트 번호 | 7 111 |
6 110 |
5 101 |
4 100 |
3 011 |
2 010 |
1 001 |
| 해밍 코드 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
결과적으로 데이터 1100에 해당하는 해밍 코드는
1100001이 된다
이때 이 코드가 맞는지 확인할려면 신드롬 비트를 계산하면 된다
신드롬 비트란 짝수 패리티와 해당하는 패리티 비트를 동시 고려한 값이다
위의 값으로 계산하면
첫자리 = 자신, 나머지는 패리티 비트값
s1 = 1, 3, 5, 7
s2 = 2, 3, 6, 7
s3 = 3, 5, 6, 7
이고 이를 계산하면
s1 = 1, 3, 5, 7 => 1 0 0 1 = 0
s2 = 2, 3, 6, 7 => 0 0 1 1 = 0
s3 = 3, 5, 6, 7 => 0 0 1 1 = 0
이 되어 s3s2s1의 값이 000이고, 이는 오류가 없음을 뜻한다
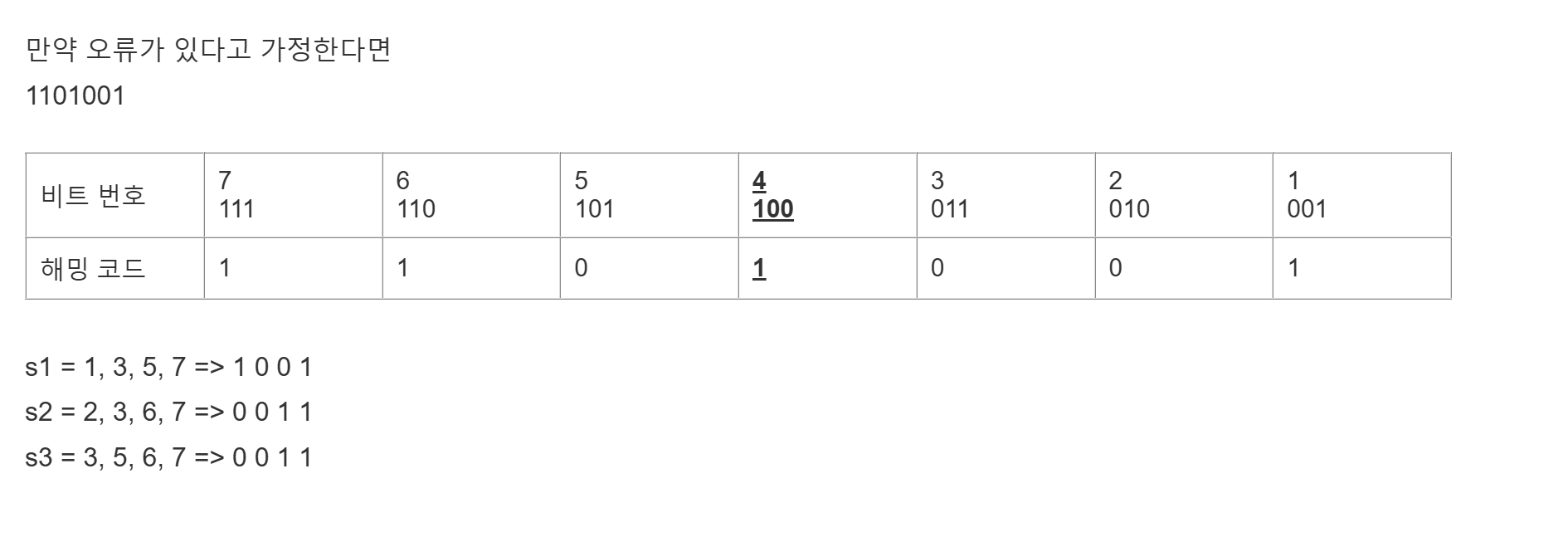
만약 오류가 있다고 가정한다면
1110001
| 비트 번호 | 7 111 |
6 110 |
5 101 |
4 100 |
3 011 |
2 010 |
1 001 |
| 해밍 코드 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
s1 = 1, 3, 5, 7 => 1 0 1 1 = 1
s2 = 2, 3, 6, 7 => 0 0 1 1 = 0
s3 = 3, 5, 6, 7 => 0 1 1 1 = 1
이 되어
s3s2s1이 101이 되고 이는 5번째 비트에 문제가 있음을 알려준다
의문점
1101001
과 같이 반전시키면
싵드롬 비트에도 정상으로 통과가 된다