네트워크 (2025 11 06)

이전

신호를 그래프로 정리

sin, cos로 보기 불편하기 때문에 Euler의 공식을 사용함

https://namu.wiki/w/%EC%98%A4%EC%9D%BC%EB%9F%AC%20%EA%B3%B5%EC%8B%9D

오일러 공식

 

 

오일러공식에서 주의깊게 볼만한 요소

j라는 허수를 사용함

e^j∂ = cos ∂ + jsin ∂ 이기에 복소수가 됨

 

그래프 값이 sin, cos로 보기 불편하기 때문에 Euler의 공식을 사용함

가독성 (복소수 지수값 > sin, cos값)

 

오일러공식에서 주의깊게 볼만한 요소

j라는 허수를 사용함

e^j∂ = cos ∂ + jsin ∂ 이기에 복소수가 됨

 

sin ∂는 어떻게 구할 수 있는가?

sin ∂에 대해서 오일러 공식을 역산해주면 sin ∂에 대한 값을 구할 수 있다

 

s(t)에서 cos를 오일러 공식을 사용해 제거할 수 있음

 

s(t)를 주고 2개의 신호 그래프를 그려라

단일 주파수의 정현파 신호(사인이나 코사인파) 가 푸리에 변환되었을 때의 주파수 스펙트럼

1. 위쪽 그래프 — ∣S(f)∣|S(f)|∣S(f)∣ (크기 스펙트럼)

• 수평축: 주파수 fff
• 수직축: 복소 푸리에 스펙트럼의 크기
• +f+f+f와 −f-f−f에 각각 A/2A/2A/2 높이의 스파이크(임펄스)가 있음
  → 이는 시간영역 신호가 Acos⁡(2πft+ϕ)A\cos(2\pi f t + \phi)Acos(2πft+ϕ)일 때의 특징입니다.

즉,

s(t)=Acos⁡(2πft+ϕ)s(t) = A\cos(2\pi f t + \phi)s(t)=Acos(2πft+ϕ)

의 푸리에 변환은

S(f)=A2[ejϕδ(f−f0)+e−jϕδ(f+f0)]S(f) = \frac{A}{2}\left[e^{j\phi}\delta(f - f_0) + e^{-j\phi}\delta(f + f_0)\right]S(f)=2A​[ejϕδ(f−f0​)+e−jϕδ(f+f0​)]

이고, 이때 크기 스펙트럼은 A/2A/2A/2로 대칭입니다.

---

2. 아래쪽 그래프 — ∠S(f)\angle S(f)∠S(f) (위상 스펙트럼)

• +f+f+f에서 위상은 +ϕ+\phi+ϕ
• −f-f−f에서 위상은 −ϕ-\phi−ϕ

즉, 신호의 위상 성분이 주파수축 양쪽에 서로 반대 부호로 나타납니다.

질문

어떤 신호가 시간축에서 주어질시 주파수 영역으로 어떻게 바꾸는가?

(s(t)를 어떻게 S(f)로 바꿀 수 있는가?)

 

신호의 종류

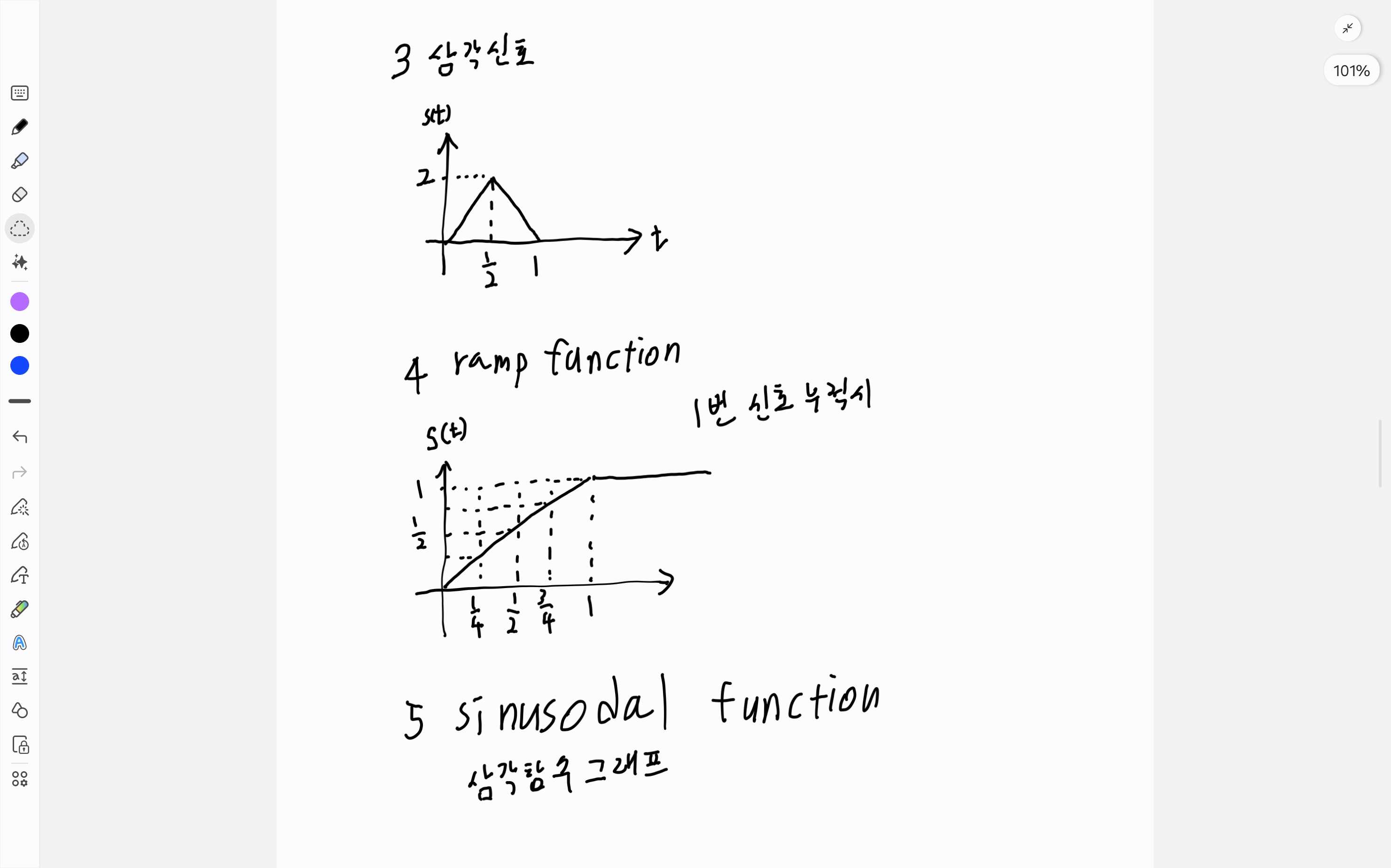
1. 사각 신호(rect function)
2. impulse function
3. 삼각신호(tri function)
4. ramp function
5. sinusodal function

 

주파수 영역으로 바꾸는 방법

푸리에 변환

s(t) -> S(f)로 변환

어떻게 하는가?